1. Theoretisches

Als "Goldenen Schnitt" bezeichnet man die Teilung einer Strecke in zwei Abschnitte in der Weise, dass sich der kleinere Abschnitt zum größeren wie der größere zur gesamten Strecke verhält.

Der größere Abschnitt soll stets bei A liegen, es gilt also:  :  =  : 

bzw. (a-x) : x = x : a

Die längere Teilstrecke  = x ist also die mittlere Proportionale zur ganzen Strecke und dem kleineren Abschnitt. Anders ausgedrückt, teilt S die Strecke  stetig; man spricht deshalb auch manchmal statt vom Goldenen Schnitt von der stetigen Teilung einer Strecke.

1.2 Bezeichnungen und Historisches

Die beiden genannten Bezeichnungen sind noch relativ jung, sie wurden erst im 19. Jahrhundert geprägt. Zum ersten Mal wird der Sachverhalt des Goldenen Schnitts von Euklid (um 300 v. Chr.) schriftlich festgehalten. Er umschreibt den Goldenen Schnitt in seiner Schrift "Elemente" im II. Buch, Satz 11, mit "Teilung nach dem äußeren und mittleren Verhältnis" und erklärt ihn mit Hilfe von Flächenanlegungen. Allerdings wird davon ausgegangen, dass die stetige Teilung und insbesondere die exakte Konstruktion der Fünfeckteilung bereits früher, z. B. bei den Ägyptern oder bei den Phytagoräern mit deren Erkennungssymbol, dem Pentagramm, bekannt war. Im Mittelalter besaß das Pentagramm nach wie vor eine mystische Symbolkraft und sollte als "Drudenfuß" vor Hexen und bösen Geistern schützen. Lucia Pacioli schreibt 1509 "De divina proportione" - "Über das göttliche Verhältnis", Kepler verwendet "sectio divina" ("göttliche Teilung").

Im letzten Jahrhundert, als man sich eingehend mit der Thematik des Goldenen Schnittes beschäftigte, entstand die Bezeichung "sectio aurea". Im Englischen findet man heute "medial section" oder "golden section", im Französischen "section d’or".

1.3 Mathematische Grundlagen

Formt man obiges Verhältnis  = 

in die quadratische Gleichung x˛ = (a-x)a ó 0 = x˛ + ax - a˛

um und löst diese nach x auf, x_1/2== 

x_1/2 = =

so erhält man für x₁ =  und für x₂ = .

Letzteres stellt keine brauchbare Lösung dar, da hier nur der innere Teilpunkt S bestimmt werden soll, d. h. D={x? 0<x<a}. Ist der größere Abschnitt x bekannt, kann a-x in Abhängigkeit von a errechnet werden:

- =  =  =  =  

Für das Verhältnis längerer Abschnitt zu kürzerem, das auch als (Major : Minor) bezeichnet wird, ergibt sich:

  =   

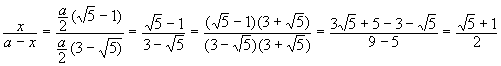
Diesen konstanten Quotienten  bezeichne ich in Zukunft aus praktischen Gründen als F . Die Konstante F steht in besonderen Beziehungen zu ihrem reziproken Wert F ^-1 =  = :

a)  F +  = b)   F -  = 1c)   ()˛ +  = 1d)    F ˛ - F = 1           Nebenrechnungen

1.4 Konstruktionsmöglichkeiten

Gegeben sei - wenn nicht anders angegeben - jeweils eine Strecke = a , die von einem gesuchten Punkt S stetig geteilt werden soll. Die Konstruktion dieses Punktes S kann auf verschiedene Arten erfolgen, eine Auswahl der "schönsten" bzw. interessantesten möchte ich hier zeigen.

Die "klassische" Konstruktion ist die einfachste und gebräuchlichste. Auf B wird eine Senkrechte = errichtet und A und C werden verbunden. Ein Kreis um C mit Radius r=schneidet  im Punkt D. Der Kreis um A mit r= schneidet im gesuchten Punkt S.
 

Beweis: ˛ = a˛ + ()˛ = a˛

==-=-

= (-1)
 
 

Ähnlich ist die ursprüngliche Konstruktion bei Euklid. Wieder konstruiert man ein rechtwinkliges Dreieck D ABC mit =a und dem dazu senkrechten =. [AC] wird über A bis D verlängert, so dass =. Der Kreis um A mit r= schneidet  im gesuchten Punkt S . (Siehe Abb. III)

Beweis: ˛ =˛ =a˛ ; =- =(-1) = 
 
 
 
 
 

Altersmäßig im Gegensatz dazu steht die folgende Konstruktionsart, die der Amerikaner George Odom erst 1982 (!) "erfand". Allerdings ist in diesem Fall =x gegeben und B wird als fehlender Punkt angenommen. Es wird ein gleichseitiges D XYZ mit der Seitenlänge 2x sowie ein Umkreis und eine Mittelparallele wie untenstehend eingezeichnet erstellt. Der Schnittpunkt des Umkreises mit AS ist B (bzw. C). Beweis:

===2x

:=:

2x := 2x : x (Vierstreckensatz)

=x

Nach dem Sehnensatz gilt:

*  =  * 

x * x = (x+) * 

x * x = (x+(a-x)) * (a-x)

x ˛ = a*(a-x)

x = (-1). S teilt  folglich im Goldenen Schnitt.
 
 

Bei folgender Konstruktion bedarf der Zeichner lediglich des Zirkels. Ob dieser Besonderheit hielt ich diese Art für unbedingt erwähnenswert.

<> Es gilt: = a = =======

<> ==a  ˛ = ˛-˛ (Pythagoras)

= ==

<>  = 2*= a==

<> ˛ =˛-˛ (Pythagoras)

=== a==

<> ˛ =˛-˛ (Pythagoras)

===

<>  =-=-=() S teilt  im Goldenen Schnitt.
 
 
 
 
 

Eine weitere Möglichkeit, die stetige Teilung zu ermitteln, besteht in der Zuhilfenahme der Wurzelschnecke. (Abb)

Mit dieser lässt sich jede , aN darstellen.   Nun kann an A auf einer beliebigen Gerade  Einheiten und bei B auf einer Parallelen 2 Einheiten abgetragen und in gewohnter "schulüblicher" Weise geteilt werden.
 

Abschließend sei in diesem Kapitel erwähnt, dass "stetige Teilung" eine einleuchtende Bezeichnung ist, da die Teilung beliebig weiter fortsetzbar ist. Beispiel:

Hat man also bereits eine im goldenen Schnitt geteilte Strecke so können beliebig viele "goldene Schnitte" nach außen oder innen abgetragen werden.

 
 
 
 
weiter zu Kapitel 2: Anwendungen in der Mathematik