Sorry, your browser doesn't support Java.  


Inhalt:

Beispielaufgaben:
1.1 Von einem rechtwinkligen Dreieck ist bekannt: c = 50, p = 32 (in beliebigen Längeneinheiten) (Abb. 1)

Berechne: a, b, q, h. Welche Kontrollen sind möglich?

Lösung:

Bei dieser Aufgabe geht es um die systematische Anwendung der Sätze:


Abb. 1
Kathetensatz:

Aus folgt
Kathetensatz:
Höhensatz:

Kontrollen:
Satz des Pythagoras:

Flächeninhalt:

 

aus: C. und H.-J. Penßel, D.Roth: Basismathematik 9 Geometrie, S. 98

1.2 In einem Dreieck ABC ist H der Höhenfusspunkt auf der Seite c.
Es gilt: und
Zeige, dass das Dreieck bei C einen rechten Winkel besitzt (Abb. 2)

Lösung:
Die Begründung wird über den Kehrsatz des Satzes des Pythagoras geführt.
Dazu muss zunächst und berechnet werden.

Satz des Pythagoras im

Satz des Pythagoras im

Abb. 2

Es folgt:

Also:

Aus dem Kehrsatz des Satzes von Pythagoras folgt daher, dass bei C ein rechter Winkel sein muss.

aus: C. und H.-J. Penßel, D.Roth: Basismathematik 9 Geometrie, S. 98f

 

Verständnisaufgaben:

2.1 Ergänze die fehlenden Terme (vgl. Abb.3). Trage dazu Deine Lösung in das leere Feld ein und klicke den - Knopf rechts davon an um sehen, ob sie richtig ist. Wenn Du die Aufgabe nicht lösen kannst, klicke auf , um die richtige Lösung der Aufgabe zu erfahren.
Hinweis: Gib als Lösung einzelne Klein- oder Großbuchstaben ein (z.B. , ). Bei Lösungen, die quadrierte Variablen enthalten, gib dies bitte mit einem "²" direkt hinter dem Buchstaben an (z.B. oder ). Drücke die Tasten "AltGr" rechts neben der Leertaste und die "2" gleichzeitig, um das Symbol "²" zu erhalten. Das kannst Du hier mal kurz ausprobieren.

Abb. 3
u² = · x
r² = s² +
t =

r² -

u² = - x²
r² = (x + y) ·
x =

r² +
- y

u² = r² -
r² = u² +
 

aus: C. und H.-J. Penßel, D.Roth: Basismathematik 9 Geometrie, S. 105


2.2 Ergänze die fehlenden Terme (vgl. Abb. 4). (schreibe Produkte direkt hintereinander zusammen. Z.B. 2m oder 3G)
f² = m² +
h · e = (i + l) ·
k² = - i²
h =

(k + ) · k

= i · l


Abb. 4

aus: C. und H.-J. Penßel, D.Roth: Basismathematik 9 Geometrie, S. 106

 

Rechenaufgaben:
3.1 Berechne den Abstand zweier Punkte P(x1|y2) und Q(x2|y2)
(siehe Abb. 5)

Bei dieser Aufgabe ist es wohl am besten, wenn Du Dir ein Blatt Papier zur Hand nimmst und dort die Aufgabe löst. Zur anschließenden Kontrolle kannst Du dann auf den Link "Lösung zeigen!" drücken. Hier wird auch der Lösungsweg erklärt, für den Fall dass Du die Aufgabe nicht verstanden hast.

Lösung zeigen!

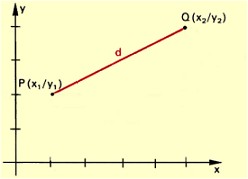Abb. 5

aus: C. und H.-J. Penßel, D.Roth: Basismathematik 9 Geometrie, S. 102


3.2 Ein Punkt B jenseits eines Flusses wird von den Punkten A und C anvisiert. Der Winkel ACB misst 90°. Der Punkt D wird so festgelegt, dass B in der Fluchtlinie von A und D liegt und außerdem ebenfalls 90° misst (Abb. 6).

Berechne den Abstand des Punktes B von A, wenn und gilt.

Nachdem Du diese Aufgabe gerechnet hast ("per Hand" auf Papier), kannst Du Dir die Richtigkeit Deiner Lösung bestätigen lassen bzw. den korrekten Lösungsweg erklären lassen.

Lösung zeigen!

Abb. 6

aus: C. und H.-J. Penßel, D.Roth: Basismathematik 9 Geometrie, S. 107

3.2 Aus der Schulaufgabensammlung:

Die Dreiecke ABC und DAC in Abb. 7 besitzen den gleichen Flächeninhalt A.

Berechne und .

Gegeben:

Lösung zeigen!


Abb. 7

aus: C. und H.-J. Penßel, D.Roth: Basismathematik 9 Geometrie, S. 112


Lösungshinweise:

Abschließende Zusammenfassung der Lösungswege:

aus: C. und H.-J. Penßel, D.Roth: Basismathematik 9 Geometrie, S. 105

 

Hilfsmittel:

Pythagoräischer Taschenrechner:

Erklärung: Mit dem pythagorischen Taschenrechner kannst Du ein pythagorisches Tripel ausrechnen, indem Du zwei der drei Zahlen eingibts und auf Lösen klickst!

Wähle dazu aus, welche der drei Seiten gesucht ist und gebe die Werte der anderen beiden ein. Drücke dann auf "Wert errechnen" und Du erhältst die Länge der dritten Seite.

(Achtung! Ergebnisse wie 1.000000002 sinnvoll auf 1 runden, da diese wegen interner Ungenauigkeit auftreten)
Seite x:
Seite y:
Seite z:

Seite
x,
y oder
z
ausrechnen

Achtung!
Überprüfe die eingegebenen Werte vor der Rechnung! Eine Eingabe wie zum Beispiel y=1 und z=1 ergibt für x keine Lösung, da z immer die Hypothenuse darstellt und somit für x keine korrekte Lösung errechnet werden kann! (Die mögliche Lösung Wurzel 2 für x ist somit nicht erlaubt, da dieser Wert größer als z wäre. Dann würde z nicht mehr die Hypothenuse, d.h. die längste Seite des Dreiecks sein!)

 


Links:

Beschr.(*)

Addresse & Titel (alle Ende Januar '99 überprüft)

Kommentar
http://www.selbst.de/sidm/archiv96/sidm_07_96/carport.htm
selbst ist der Mann - Heft 7 / 1996 - Carport-Bausatz mit Geräteraum		 die oben beschriebene Seite, auf der der Bau eines Carport beschrieben wird.


GeoNet
+

 http://did.mat.uni-bayreuth.de/seminar/internet_mu/ueb.htm
Übungen		 Seite, die mit Hilfe von GeoNet einige Aufgaben stellt.
(*) Erläuterungen:
die Seite ist in deutscher Sprache
GeoNet JAVA-Programm, mit dem man geometrische Operationen durchführen kann
+, ++ besonders empfehlenswerte Seite

Zurück zum Inhalt

(c) 1998,99 by S. Sigwart